収束と一様性¶

はじめに ¶

いくつかの環境では、スレッドのグループが同じプログラムを並列に実行し、グループ内の効率的な通信は収束演算と呼ばれる特殊なプリミティブを使用して確立されます。収束演算の結果は、それに参加するスレッドの集合に依存します。

収束の直感的なイメージは、スレッドが「ロックステップ」で実行されるという考えに基づいています。一連のスレッドは、すべてが「同じ命令シーケンスを一緒に」実行している場合、収束していると見なされます。そのようなスレッドは、分岐の差異で分岐し、後で共通のプログラムポイントで再収束する可能性があります。

この直感的なイメージでは、収束したスレッドが命令を実行すると、その結果の値は、それらのスレッドで同じであれば一様であり、そうでなければ分岐しているとされます。同様に、ブランチはその条件が一様であれば一様ブランチであり、そうでなければ分岐ブランチです。

しかし、ロックステップ実行の仮定は、収束演算での通信を記述するために必要ではありません。また、そのような並列環境でスレッドがどのように実行されるかを過剰に指定することにより、実装（コンパイラとハードウェアの両方）を制約します。この仮定を排除するために

収束を、異なるスレッドによる各命令の実行間の関係として定義し、スレッド自体間の関係としては定義しません。この定義は既知のターゲットに対して妥当であり、LLVM IRにおける収束演算のセマンティクスと互換性があります。
一様性もこの収束の観点から定義します。命令の出力は、その命令の対応する実行が収束している場合にのみ、複数のスレッドにわたって一様性を調べることができます。

このドキュメントでは、関数内の各命令での収束を決定するための静的解析について説明します。この解析は、還元不可能な制御フローをカバーするように、以前の分岐解析に関する作業[DivergenceSPMD]を拡張したものです。説明されている解析は、LLVM IRまたはMIR関数内の各命令で計算された値の（複数）の一様性を決定するUniformityAnalysisを実装するためにLLVMで使用されます。

[DivergenceSPMD]

Julian Rosemann、Simon Moll、およびSebastian Hack。2021年。還元可能な制御フローグラフにおけるSPMD分岐のための抽象解釈。Proc。ACM プログラム。Lang。5、POPL、記事31（2021年1月）、35ページ。https://doi.org/10.1145/3434312

動機 ¶

分岐の差異は、CFGの変更や収束演算のCFG内の異なるポイントへの移動など、プログラム変換を制約します。分岐の差異にわたってこれらの変換を実行すると、収束して収束演算を実行するスレッドの集合が変更される可能性があります。これらの制約はこのドキュメントの範囲外ですが、一様性解析により、これらの制約が保持されない一様ブランチを特定できます。

一様性は、共有実行リソース（例：ウェーブ、ワープ、またはサブグループ）を持つグループでスレッドを実行するターゲットでも、それ自体で役立ちます。

一様な出力は、共有リソースで計算または保存できる可能性があります。
これらのターゲットは、ブランチの各側が同じグループ内の対応するスレッドによって続かれるように、分岐の差異を「線形化」する必要があります。しかし、グループ全体のスレッドがブランチのどちらか一方に従うため、一様ブランチでは線形化は不要です。

用語 ¶

サイクル: LLVMサイクル用語で説明されています。
閉じたパス: 閉じたパスとサイクルで説明されています。
非連結パス: CFG内の2つのパスは、両方に共通するノードが開始ノードまたは終了ノード、またはその両方のみである場合、非連結であると言われます。
結合ノード: ブランチの結合ノードはそのブランチから始まる非連結パスに沿って到達可能なノードです。
分岐パス: 分岐パスは、分岐の差異から始まり、ブランチの結合ノードに到達するか、ブランチの結合ノードを通過せずに関数の最後まで到達するパスです。

スレッドと動的インスタンス ¶

プログラムソース内の命令の各出現は、静的インスタンスと呼ばれます。スレッドがプログラムを実行すると、静的インスタンスの実行ごとに、その命令の異なる動的インスタンスが生成されます。

各スレッドは一意の動的インスタンスシーケンスを生成します。

シーケンスは、ブランチの決定とループのトラバーサルに沿って生成されます。
「最初の」命令の動的インスタンスで開始します。
連続する「次の」命令の動的インスタンスで続けます。

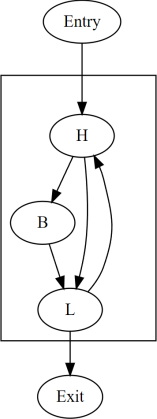
スレッドは独立しています。一部のターゲットでは、可能であればリソースを共有するために、グループで実行することを選択する場合があります。

		1	2	3	4	5	6	7	8	9
スレッド1	Entry1	H1	B1	L1	H3		L3				Exit
スレッド2	Entry1	H2		L2	H4	B2	L4	H5	B3	L5	Exit

上記の表では、各行が異なるスレッドであり、そのスレッドによって左から右に生成された動的インスタンスをリストしています。各スレッドは、Entryノードで始まりExitノードで終わる同じプログラムを実行しますが、異なるスレッドはプログラムの制御フローを通して異なるパスを取る可能性があります。列は便宜上番号が付けられており、空のセルには特別な意味はありません。同じ列にリストされている動的インスタンスは収束しています。

収束 ¶

収束前は、動的インスタンスに対する厳密な部分順序であり、次のように定義されます。

動的インスタンスPが同じスレッド内でQの前に実行される場合、PはQ収束前です。
動的インスタンスPが同じスレッド内でQ1の前に実行され、Q1がQ2と収束している場合、PはQ2収束前です。
動的インスタンスP1がP2と収束し、P2が同じスレッド内でQの前に実行される場合、P1はQ収束前です。

	1	2	3	4	5	6	7	8	9
スレッド1	Entry	…				S2	T	…	Exit
スレッド2	Entry	…		Q2	R	S1		…	Exit
スレッド3	Entry	…	P	Q1				…

上記の表は、異なるスレッドからの動的インスタンスの部分シーケンスを示しています。同じ列の動的インスタンスは、収束していると仮定されます（つまり、収束関係で互いに関連しています）。結果として得られる収束順序には、エッジP -> Q2、Q1 -> R、P -> R、P -> Tなどが含まれます。

収束は、同じ静的インスタンスに対して異なるスレッドによって生成された動的インスタンスに対する推移的な対称関係です。

異なる環境が異なる方法で動的インスタンスを関連付ける可能性があるため、収束関係に対する単一の定義を提供することは実際的ではありません。収束前が厳密な部分順序であるという事実は、収束関係に対する制約です。異なる動的インスタンスが決して収束しない場合、これは自明に満たされます。以下では、最大収束と呼ばれる関係を示します。これは収束前を満たし、既知のターゲットに適しています。

注記

収束前関係は直接観測できません。プログラム変換は一般的に、それが明らかに収束前関係を変更するとしても、命令の順序を変更できます。
収束した動的インスタンスは、同時に、または同じリソースで実行される必要はありません。収束演算の収束した動的インスタンスはそう見えるかもしれませんが、それは実装の詳細です。
PがQ収束前であるという事実は、メモリモデルの意味でPがQ前に発生することを自動的に意味するものではありません。

最大収束 ¶

このセクションでは、厳密な収束前順序に違反することなく、最大収束関係を生成するために使用できる制約を定義します。この最大収束関係は、実際のターゲットに対して妥当であり、収束演算と互換性があります。

最大収束関係は、スレッドがサイクルの各「反復」でヘッダーで収束するという仮定の下で、サイクルヘッダーの観点から定義されます。非公式には、サイクルの同じ反復を実行する2つのスレッドは、そのサイクルに入った後、サイクルヘッダーを同じ回数実行したことがあれば、両方ともです。一般に、これは親サイクルの反復も考慮する必要があります。

最大収束

同じ静的インスタンスXに対して異なるスレッドによって生成された動的インスタンスX1とX2は、次の場合にのみ、最大収束関係で収束します。

Xはどのサイクルにも含まれていないか、または

Xを含むヘッダーHを持つ各サイクルCに対して

それぞれのスレッドにおいて、X1の前に存在するHの全ての動的インスタンスH1は、X2に対してconvergence-beforeであり、

それぞれのスレッドにおいて、X2の前に存在するHの全ての動的インスタンスH2は、X1に対してconvergence-beforeです。

X1とX2がconvergedであると仮定しません。

注記

CFGが既約である場合、サイクルヘッダーは特定のCFGに対して一意とは限りません。同じCFGに対する各サイクル階層は、異なる最大converged-with関係をもたらします。

簡潔にするため、このドキュメントの残りの部分では、用語「converged」は、「与えられたサイクル階層に対する最大converged-with関係の下で関連付けられる」ことを意味するものとします。

上記の例では、最大収束を次のように示すことができます。

		1	2	3	4	5	6	7	8	9
スレッド1	Entry1	H1	B1	L1	H3		L3				Exit
スレッド2	Entry2	H2		L2	H4	B2	L4	H5	B3	L5	Exit

Entry1とEntry2はconvergedです。
H1とH2はconvergedです。
B1とB2は、B1に対してconvergence-beforeではないH4が存在するため、convergedではありません。
H3とH4はconvergedです。
H3とH5は、H3に対してconvergence-beforeではないH4が存在するため、convergedではありません。
L1とL2はconvergedです。
L3とL4はconvergedです。
L3とL5は、L3に対してconvergence-beforeではないH5が存在するため、convergedではありません。

サイクルヘッダーへの依存性 ¶

convergence-beforeにおける矛盾は、あるサイクル内にある2つのノード間でのみ発生する可能性があります。そのようなノードの動的インスタンスは、同じスレッド内でインターリーブされる可能性があり、このインターリーブはスレッドによって異なる場合があります。

スレッドがノードXを一度実行し、その後再び実行する場合は、Xを含むCFG内の閉じたパスをたどっている必要があります。そのようなパスは、少なくとも1つのサイクル（閉じたパス全体を含む最小のサイクル）のヘッダーを通過する必要があります。特定のスレッドでは、Xの2つの動的インスタンスは、少なくとも1つのサイクルヘッダーの実行によって区切られるか、X自体がサイクルヘッダーです。

既約サイクル（自然ループ）では、ヘッダーの実行は、サイクルの新しい反復の開始に相当します。しかし、今後の作業で説明されているような、converged-with関係に対する明示的な制約が存在する場合、このアナロジーは成り立ちません。代わりに、サイクルヘッダーは、最大converged-with関係における暗黙的な収束点として扱う必要があります。

C1、C2、…、Ckという入れ子になったサイクルのシーケンスを考えます。C1は最も外側のサイクルであり、Ckは最も内側のサイクルであり、それぞれヘッダーH1、H2、…、Hkを持ちます。スレッドがサイクルCkに入ると、次のいずれかが可能です。

スレッドは、ヘッダーH1からHkのいずれも実行せずに、直接サイクルCkに入りました。
スレッドは、入れ子になったヘッダーの一部またはすべてを1回以上実行しました。

最大converged-with関係は、サイクルに関する次の直感を捉えています。

2つのスレッドがトップレベルのサイクルC1に入ると、C1の子である子ノードのすべてのノードのconverged動的インスタンスを実行します。
2つのスレッドが入れ子になったサイクルCkに入ると、いずれかのスレッドがCkを終了するまで、Ckの子であるすべてのノードのconverged動的インスタンスを実行します。これは、いずれかのスレッドが遭遇した最後の入れ子になったヘッダーのconverged動的インスタンスを実行した場合に限ります。

スレッドが入れ子になったサイクルCkを終了する場合、それを再入力するには、Ckの外側の閉じたパスをたどる必要があります。これには、前述のように、いくつかの外側のサイクルのヘッダーを実行する必要があります。

入れ子になったサイクルCkの子であるノードXに対して、スレッドT1とT2によって生成された2つの動的インスタンスX1とX2を考えます。最大収束は、X1とX2を次のように関連付けます。

いずれのスレッドもH1からHkまでのヘッダーを1つ実行しなかった場合、X1とX2はconvergedです。
そうでない場合、H1からHkまでのヘッダーQ（QはXと同じ可能性があります）のconverged動的インスタンスQ1とQ2がなく、Q1がX1の前に、Q2がX2の前にそれぞれのスレッドで発生する場合、X1とX2はconvergedではありません。
そうでない場合、H1からHkまでのヘッダーQのconverged動的インスタンスのペアQ1とQ2を考えます。これは、それぞれのスレッドにおいてX1とX2の直前に最も最近発生します。その後、スレッドT1においてQ1とX1の間に、またはスレッドT2においてQ2とX2の間に、H1からHkまでのヘッダーの動的インスタンスがない場合、X1とX2はconvergedとなります。言い換えれば、Q1とQ2は最後の収束点を表し、Xを実行する前に他のヘッダーは実行されません。

例

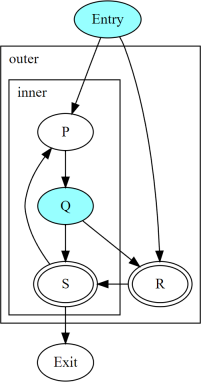
_images/convergence-both-diverged-nested.png

上の図は、ヘッダーRとSを持つ2つの入れ子になった既約サイクルを示しています。ノードEntryとQは分岐しています。以下の表は、CFGを通る異なるパスを取る3つのスレッド間の収束を示しています。同じ列にリストされている動的インスタンスはconvergedです。

1

2

3

4

5

6

7

8

10

スレッド1

Entry

P1

Q1

S1

P3

Q3

R1

S2

Exit

スレッド2

Entry

P2

Q2

R2

S3

Exit

スレッド3

Entry

R3

S4

Exit

P2とP3はS1が存在するためconvergedではありません。
Q2とQ3はS1が存在するためconvergedではありません。
S1とS3はR2が存在するためconvergedではありません。
S1とS4はR3が存在するためconvergedではありません。

非公式には、T1とT2は、外側のループのヘッダーを実行することなく、異なる回数だけ内側のループを実行します。すべてのスレッドは、初めて外側のループのヘッダーを実行した時点で、外側のループで合流します。

均一性 ¶

2つの収束した動的インスタンスの出力は、それら2つの動的インスタンスで比較して等しい場合に限り、均一です。
静的インスタンスXの出力は、特定のスレッド集合に対して、それらのスレッドによって生成されたXのすべての収束した動的インスタンスのペアに対して均一である場合に限り、均一です。

非均一な値は、分岐していると言われます。

スレッドの集合Sに対して、静的インスタンスの各出力の均一性は、次のように決定されます。

命令のセマンティクスによって、出力は均一であると指定される場合があります。
それ以外の場合、静的インスタンスがm-収束していない場合、出力は分岐します。
それ以外の場合、静的インスタンスがm-収束している場合
1. PHIノードである場合、その出力は、S内のすべてのスレッドによって生成されたすべての収束した動的インスタンスのペアに対して、
  1. 両方のインスタンスが収束した動的インスタンスから同じ出力を選択し、かつ、
  2. その出力がS内のすべてのスレッドに対して均一である場合に限り、均一です。
2. それ以外の場合、出力は、入力オペランドがS内のすべてのスレッドに対して均一である場合に限り、均一です。

分岐ループの終了 ¶

ループ内で分岐が発生した場合、分岐したパスがループの終了まで続く可能性があります。これは、分岐ループの終了と呼ばれます。ループが既約である場合、分岐したパスは再入し、最終的にループ内の結合に到達する可能性があります。このような結合については、分岐エントリ基準を調べる必要があります。

ループの外側にある分岐パスのノードは、ループ内で収束して実行されている2つのスレッドが均一な値を生成するが、ヘッダーを異なる回数実行した後に（非公式には、ループの異なる反復で）同じ分岐パスに沿ってループから終了する場合、時間的分岐を経験します。ループ内のノードNに対しては、2つのスレッドの出力は均一である可能性がありますが、ループの外側の任意の利用Uは、Nの非収束動的インスタンスから値を受け取ります。Uの出力は、命令のセマンティクスに応じて、分岐する可能性があります。

静的均一性解析 ¶

既約制御フローは、深さ優先探索中のヘッダーの選択に応じて、異なるループ階層をもたらします。その結果、静的解析では、既約ループ内のノードの収束を常に決定できず、均一性解析は、その収束がループ階層に依存しない静的インスタンスに限定されます。

m-収束静的インスタンス

静的インスタンスXは、その動的インスタンスに対する最大の収束関係が、そのCFGに対して構築できるすべてのループ階層で同じである場合に限り、特定のCFGに対してm-収束します。

注記

言い換えれば、m-収束静的インスタンスXの2つの動的インスタンスX1とX2は、あるループ階層で収束している場合に限り、同じCFGの他のすべてのループ階層でも収束しています。

前述のように、簡潔にするために、「収束」という用語は、特定のループ階層に対する最大の収束関係の下で関連付けられていることを意味するものに限定します。

特定のCFG内の各ノードXは、Xを含むすべてのループが次の必要条件を満たす場合に限り、m-収束していると報告されます。

ループ内のすべての分岐は、分岐エントリ基準を満たし、かつ、

ループの外側の分岐からループに到達する分岐パスはありません。

注記

既約ループは、自明に上記の条件を満たします。特に、CFG全体が既約である場合、CFG内のすべてのノードはm-収束します。

静的インスタンスの各出力の均一性は、前述の基準を使用して決定されます。分岐出力の検出により、その使用（分岐を含む）も分岐する可能性があります。解析はこの分岐を固定点に達するまで伝播します。

これらの基準を使用して推論された収束は、任意のループ階層に対する最大の収束関係の安全な部分集合です。特に、他のループ階層T'を調べたときにその事実が検出されなくても、特定のループ階層Tに対して静的インスタンスがm-収束しているかどうかを判断するのに十分です。

このプロパティにより、コンパイラ変換は、基礎となるループ解析で行われたDFSの選択に影響されることなく、均一性解析を使用できます。2つの変換が同じCFGに対して均一性解析の異なるインスタンスを使用する場合、ある解析インスタンスでの「分岐値」の結果は、別のインスタンスでの「均一値」の結果と矛盾することはありません。

SimplifyCFG、CSE、ループ変換などの一般的な変換は、プログラムを最大の収束関係を変更する方法で変更します。これはまた、以前は均一だった値が、そのような変換の後で分岐する可能性があることを意味します。そのような変換の後では、均一性を再計算する必要があります。

ループ内の分岐 ¶

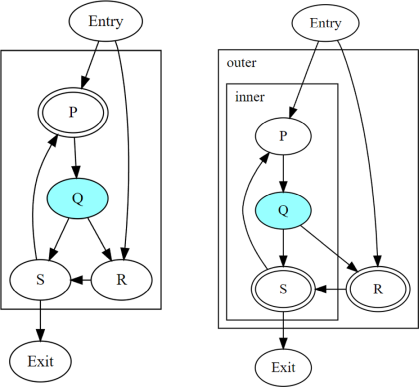
_images/convergence-divergent-inside.png

上の図は、既約循環領域内の分岐Qを示しています。Qで2つのスレッドが分岐する場合、循環領域内の動的インスタンスの収束は、選択されたループ階層に依存します。

ヘッダーPを持つ単一ループCを検出する実装では、ループ内の収束はPによって決定されます。
ヘッダーRとSを持つ2つの入れ子になったループを検出する実装では、それらのループ内の収束は、それぞれのヘッダーによって決定されます。

保守的なアプローチとしては、既約ループ内のすべてのノードを出力が分岐していると報告することです。しかし、均一性を最大限にするために、CFG内のm-収束ノードを認識することが望ましいです。このセクションでは、閉じたパスから導出されるノードのそのようなパターンの1つについて説明します。閉じたパスはCFGのプロパティであり、ループ階層には依存しません。

分岐エントリ基準

閉じたパスP内のすべてのノードの動的インスタンスは、すべての分岐Bとその結合ノードJがP上にある場合に限り、m-収束します。BからJへの分岐パス上に存在するPへのエントリはありません。

上の図の閉じたパスP -> Q -> R -> Sを考えてみます。PとRは閉じたパスへのエントリです。Qは分岐であり、Sはその分岐の結合であり、分岐パスQ -> R -> SとQ -> Sがあります。

分岐エントリRが存在する場合、あるループ階層では、Rは閉じたパスと子ループC'を含む最小のループCのヘッダーであり、C - Rの集合に存在し、分岐Qと結合Sの両方を含みます。スレッドがQで分岐する場合、サブセットMの1つはループC'内で継続する一方で、補集合NはC'を終了し、Rに到達します。Rの存在により、集合M内のスレッドによって実行されたSの動的インスタンスは、集合N内で実行されたものとは収束しません。非公式には、Qで分岐したスレッドは、外側のループCの同じ反復で再収束しますが、内側のループC'を異なる方法で実行している可能性があります。

1

2

3

4

5

6

7

8

9

10

11

スレッド1

Entry

P1

Q1

R1

S1

P3

…

Exit

スレッド2

Entry

P2

Q2

S2

P4

Q4

R2

S4

Exit

上の表において、R1のためにS2はS1と収束していません。

もしRが存在しないか、R以外のノードがCのヘッダーである場合、そのような子サイクルC'は検出されません。Qで分岐するスレッドは、QからSへの任意のパス上でサイクルヘッダーに遭遇しないため、Sの収束した動的インスタンスを実行します。非公式には、Qで分岐するスレッドは、Cの同じ反復でSで再収束します。

1

2

3

4

5

6

7

8

9

10

スレッド1

Entry

P1

Q1

R1

S1

P3

Q3

R3

S3

Exit

スレッド2

Entry

P2

Q2

S2

P4

Q4

R2

S4

Exit

注記

一般に、上記の記述におけるサイクルCは、異なるヘッダーに対して同じサイクルになることは期待されていません。サイクルとそのヘッダーは密接に関連しています。同じ最外側のサイクル内の異なるヘッダーの場合、検出される子サイクルは異なる場合があります。上記の例に関連する特性は、すべての閉じたパスに対して、そのパスを含み、そのパス上にヘッダーを持つサイクルCが存在することです。

分岐エントリ基準は、分岐Bとその結合Jを通過するすべての閉じたパスに対してチェックする必要があります。すべての閉じたパスは、あるサイクルのヘッダーを通過するため、これはBとJを含むすべてのサイクルCをチェックすることに相当します。Cのヘッダーが結合Jを支配する場合、ヘッダーからJへの任意のパスへのエントリは存在せず、これにはBからJへの任意の分岐パスが含まれます。これは、Cを含む外側のサイクルのヘッダーを通過するすべての閉じたパスにも当てはまります。

したがって、分岐エントリ基準は、次のように保守的に簡素化できます。

分岐Bとその結合ノードJについて、BとJの両方を含むサイクルC内のノードは、次の場合にのみm-収束します。

BがJを厳密に支配するか、

CのヘッダーHがJを厳密に支配するか、

再帰的に、同じ条件を満たすC内のサイクルC'が存在します。

JがHまたはBと同じである場合、自明な支配は、分岐パスへのエントリについて何らかの記述を行うには不十分です。

サイクルに到達する分岐パス ¶

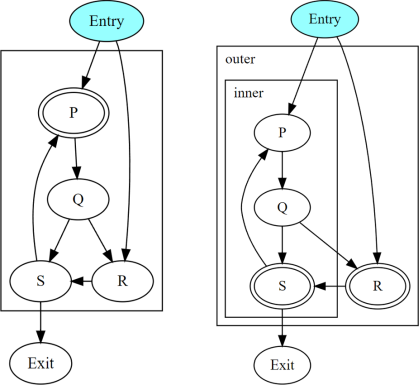
_images/convergence-divergent-outside.png

図は、Qの代わりにEntryに分岐がある2つのサイクル階層を示しています。P -> Q -> R -> Sという閉じたパスにそれぞれPとRで入る2つのスレッドの場合、パスに沿って生成される動的インスタンスの収束は、PまたはRのどちらがヘッダーであるかによって異なります。

Pがヘッダーである場合の収束。

1

2

3

4

5

6

7

8

9

10

11

12

13

スレッド1

Entry

P1

Q1

R1

S1

P3

Q3

S3

Exit

スレッド2

Entry

R2

S2

P2

Q2

S2

P4

Q4

R3

S4

Exit
Rがヘッダーである場合の収束。

1

2

3

4

5

6

7

8

9

10

11

12

スレッド1

Entry

P1

Q1

R1

S1

P3

Q3

S3

Exit

スレッド2

Entry

R2

S2

P2

Q2

S2

P4

…

Exit

したがって、分岐パスがサイクルの外部から既約サイクルの異なるエントリに到達する場合、静的解析はサイクル内のすべてのノードをm-収束していないと保守的に報告します。

既約サイクル ¶

CがヘッダーHを持つ既約サイクルである場合、任意のDFSにおいて、Hは Cを含むあるサイクルC'のヘッダーでなければなりません。DFSに依存せず、H自身以外のサブグラフCへのエントリはありません。したがって、次のようなことが言えます。

分岐と結合の両方ともサブグラフC内にある場合、分岐エントリ基準は自明に満たされます。
分岐パスが外部からサブグラフCに到達する場合、その収束は常に同じヘッダーHによって決定されます。

明らかに、これはCが既約サイクルとして検出されるサイクル階層Tでのみ決定できます。 Cが同じヘッダーを持つより大きなサイクルC'の一部である異なるサイクル階層T'ではそのような結論を出すことはできませんが、これはTにおける結論と矛盾しません。

制御された収束 ¶

収束制御トークンは、プログラム内の特定の時点でどのスレッドが収束しているかを決定するための明示的なセマンティクスを提供します。この影響は、動的インスタンス上の制御された最大収束関係と、静的インスタンスの制御されたm-収束プロパティに組み込まれています。均一性分析は、収束制御トークンをサポートするターゲットについて、LLVMに実装されています。

ドキュメント

参加方法

追加リンク

このページ