LLVM サイクル用語

サイクル

サイクルは、LLVM ループ の一般化であり、以下のように再帰的に定義されます [HavlakCycles]

  1. 関数CFGまたはその部分グラフである有向グラフGにおいて、サイクルとは、少なくとも1つの内部エッジを持つ最大強連結領域です。(参考情報 — 少なくとも1つの内部エッジが必要であるという要件により、単一の基本ブロックがサイクルとなるのは、その基本ブロック自身に戻るエッジが存在する場合のみです。)

  2. サイクル内の基本ブロックで、サイクル内の他の基本ブロックにアクセスせずに関数のエントリからパスに沿って到達できるものを、サイクルのエントリと呼びます。サイクルには複数のエントリが存在する場合があります。

  3. 関数のエントリから始まる特定の深さ優先探索について、最初に訪問されるサイクルのノードを、この特定のDFSに関するそのサイクルのヘッダと呼びます。ヘッダは常にエントリノードです。

  4. 関数のエントリから始まる任意の深さ優先探索において、CFGで見つかったサイクルの集合は同じです。これらは、それ自体に親を持たないトップレベルサイクルです。

  5. ヘッダHを持つサイクルCの中にネストされた子サイクル（または単にサイクル）とは、ノードの集合（C - H）上で誘導された部分グラフ内のサイクルです。Cはこれらのサイクルの親であると言われます。

したがって、サイクルは実装定義のフォレストを形成し、各サイクルCは、Cの中にネストされた任意の子サイクルの親となります。このツリーは、同じ関数内のループのネストを密接に反映しています。縮約可能サイクル（LLVMループ）Lの一意のエントリは、その他のすべてのノードを支配し、使用されるDFSツリーに関係なく、常にいくつかのサイクルCのヘッダとして選択されます。このサイクルCはループLのスーパーセットです。非縮約可能サイクルの場合、エントリノードのいずれもサイクルのノードを支配しません。エントリノードの1つが、実装定義の方法で、サイクルのヘッダとして選択されます。

サイクルが複数のエントリを持つ場合、非縮約可能であり、そうでない場合は縮約可能です。

サイクルCが基本ブロックBの親であるとは、BがCに存在するがCの子サイクルには存在しない場合を指します。その場合、BはサイクルCの子でもあると言われます。

基本ブロックまたはサイクルXが、いかなるサイクルの子でもない場合、トップレベルブロックと呼ばれます。

基本ブロックまたはサイクルXが、別の基本ブロックまたはサイクルYの兄弟であるとは、両方が親を持たないか、または両方が同じ親を持つ場合を指します。

参考情報

  • サイクルのヘッダ以外のエントリブロックは、子サイクルに含まれる可能性があります。

  • CFGが縮約可能な場合、サイクルはまさに自然ループであり、すべてのサイクルは正確に1つのエントリブロックを持ちます。

  • サイクルは（定義により）適切にネストされています。

  • サイクルのエントリブロックは、支配木において兄弟です。

[HavlakCycles]

Paul Havlak, “Nesting of reducible and irreducible loops.” ACM Transactions on Programming Languages and Systems (TOPLAS) 19.4 (1997): 557-567.

サイクルの例

自然ループを含む非縮約可能サイクル

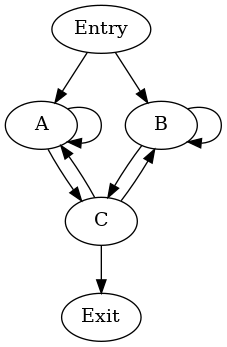
_images/cycle-1.png

AとBの自己ループは、2つのシングルブロックの自然ループを生み出します。サイクルの可能な階層は次のとおりです。

cycle: {A, B, C} entries: {A, B} header: A
- cycle: {B, C}  entries: {B, C} header: C
  - cycle: {B}   entries: {B}    header: B

この階層は、DFSがブロックをA、C、Bの順序（プリオーダー）で訪問する場合に発生します。

2つの自然ループの非縮約可能な和集合

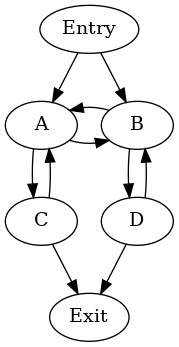
_images/cycle-2.png

2つの自然ループがあります：{A, C}と{B, D}。サイクルの可能な階層は次のとおりです。

cycle: {A, B, C, D} entries: {A, B} header: A
- cycle: {B, D}     entries: {B}    header: B

自然ループを含まない非縮約可能サイクル

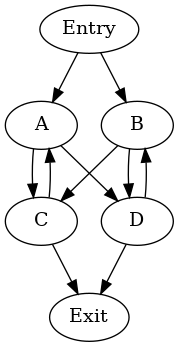
_images/cycle-3.png

このグラフには自然ループが含まれていません — ノードA、B、C、Dは支配木で兄弟です。サイクルの可能な階層は次のとおりです。

cycle: {A, B, C, D} entries: {A, B} header: A
- cycle: {B, D}     entries: {B, D} header: D

閉路とサイクル

CFGにおける閉路とは、CFG内のノードとエッジの連結されたシーケンスであり、開始ノードと終了ノードが同じであり、残りの（内部の）ノードは異なるものです。

閉路Pへのエントリとは、P上のノードであり、P上の他のノードを通過せずに関数エントリから到達可能なノードです。

  1. ノードDが閉路P内の1つ以上のノードを支配し、PがDを含まない場合、DはP内のすべてのノードを支配します。

    証明：UをDによって支配されるP内のノードとします。Dによって支配されないP内のノードVが存在する場合、UはDを通過せずにVを介して関数エントリノードから到達可能になり、これはDがUを支配するという事実と矛盾します。

  2. ノードDが閉路P内の1つ以上のノードを支配し、PがDを含まない場合、Pを含むがDを含まないサイクルCが存在します。

    証明：上記の性質から、DはP内のすべてのノードを支配します。実装定義のDFSによって検出されたサイクルのネストについて、Pを含む最小のサイクルCを検討します。矛盾のために、DがCにあると仮定します。すると、サイクルのヘッダは、サイクル内の他のノードによって支配されることができないため、CのヘッダHはPに存在できません。したがって、Pは集合（C-H）にあり、Pを含むさらに小さいサイクルC’がCに存在しなければなりませんが、それはCの選択方法と矛盾します。

  3. 閉路PがノードU1とU2を含み、それぞれそれらの支配者D1とD2を含まない場合、U1とU2を含むがD1とD2のどちらも含まないサイクルCが存在します。

    証明：上記の性質から、各D1とD2は別々にP内のすべてのノードを支配します。Pを含むがD1（それぞれD2）を含まないサイクルC1（それぞれC2）が存在します。C1とC2は同じサイクルであるか、または一方のサイクルがもう一方のサイクルの中にネストされています。したがって、常にU1とU2を含み、D1とD2のどちらも含まないサイクルが存在します。

  1. 任意のサイクル階層において、閉路Pを含む最小のサイクルCのヘッダHは、P上にあります。

    証明：HがPにない場合、Pを含むC - Hの集合内にさらに小さいサイクルC’が存在し、Cがそのような最小のサイクルであるという主張と矛盾します。

縮約可能サイクルヘッダ

サイクル階層は選択されたDFSに依存しますが、縮約可能サイクルは次の不変式を満たします。

ヘッダHを持つ縮約可能サイクルCが任意のDFSで検出された場合、HをヘッダとするサイクルC’がすべてのDFSに存在し、Cを含みます。

証明：Hを通過するC内の閉路Pについて、すべてのサイクル階層には、Pを含む最小のサイクルC’があり、そのヘッダはPにあります。HはPへの唯一のエントリであるため、HはC’のヘッダでなければなりません。ヘッダはサイクルを一意に定義するため、C’はすべてのそのような閉路Pを含み、したがってC’はCを含みます。